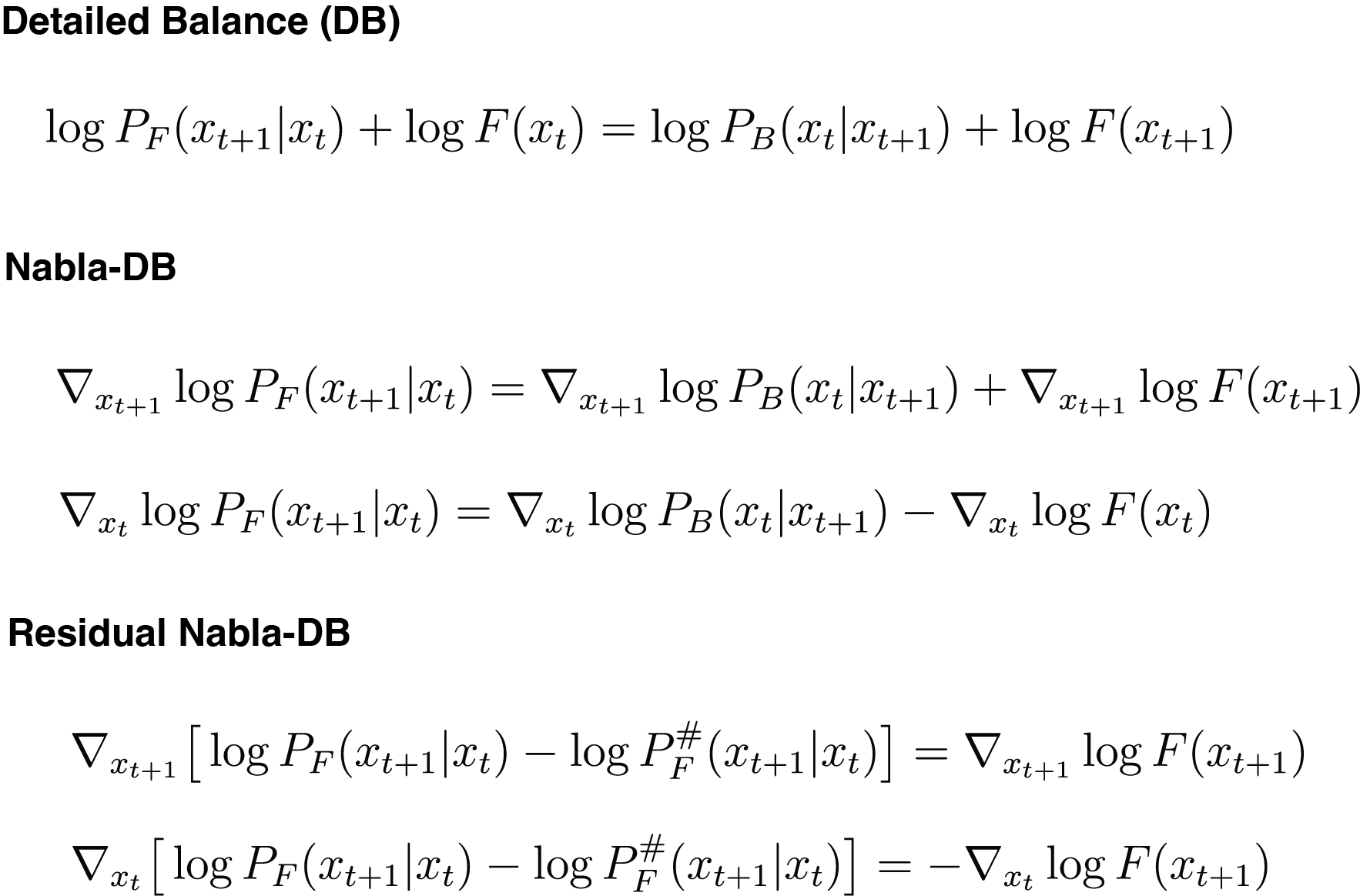While one commonly trains large diffusion models by collecting datasets on target downstream tasks, it is often desired to align and finetune pretrained diffusion models on some reward functions that are either designed by experts or learned from small-scale datasets. Existing methods for finetuning diffusion models typically suffer from lack of diversity in generated samples, lack of prior preservation, and/or slow convergence in finetuning. 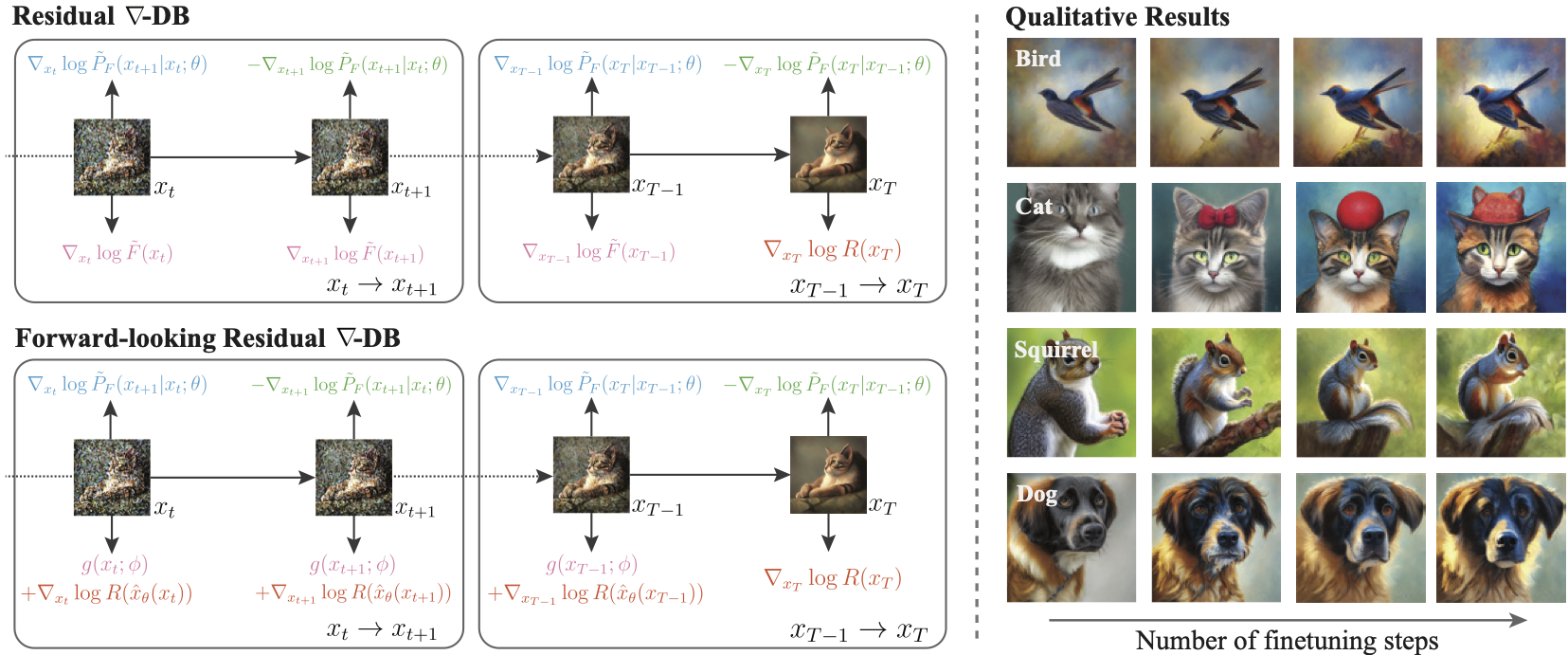Inspired by recent successes in generative flow networks (GFlowNets), a class of probabilistic models that sample with the unnormalized density of a reward function, we propose a novel GFlowNet method dubbed Nabla-GFlowNet (abbreviated as \methodname), together with an objective called \graddb, plus its variant \resgraddb for finetuning pretrained diffusion models. These objectives leverage the rich signal in reward gradients for diversity- and prior-aware finetuning. We show that our proposed method achieves fast yet diversity- and prior-preserving finetuning of Stable Diffusion, a large-scale text-conditioned image diffusion model, on different realistic reward functions.
We finetune all models for 200 update steps and pick the model with the best reward but without collapsed samples.
We treat the inference process of a diffusion model as a GFlowNet, which satisfies the Detailed Balance (DB) condition: the forward (denoising) PF and the backward (noising) PB process must be bridged by a function called the flow function F(x_t).
From the DB condition, we derive the equivalent gradient-informed ∇-DB condition that is better suited for diffusion models.
Given a pretrained model PF# as the prior, we further derive the Residual ∇-DB condition.
